Algorithm

Algorithm_SW문제해결

Sergemeow 2023. 4. 10. 16:58

문제해결 과정

  • 문제를 읽고 이해
  • 문제를 익숙한 용어로 재정의
  • 어떻게 해결할지 계획을 세움
  • 계획을 검증
  • 프로그램으로 구현
  • 풀이를 돌아보고 개선 방법 여부 확인

복잡도 분석

  • Big-Oh 표기
    • O-표기는 복잡도의 점근적 상한을 나타냄
    • 복잡도가 f(n) = 2N2-7n+4라면, f(n)의 O-표기는 O(n2)임
    • 먼저 f(n)의 단순화된 표현은 n2
    • 단순화된 함수 n2에 임의의 상수 c를 곱한 cn2이 n이 증가함에 따라 f(n)의 상한이 됨
  • 자주 사용하는 O- 표기
    • O(1) 상수시간 constant time
    • O(logn) 로그(대수)시간 logarithmic time
    • O(n) 선형시간 linear time
    • O(nlogn) 로그 선형시간 log-linear time
    • O(n2) 제곱시간 quadratic time
    • O(n3) 세제곱시간 cubic time
    • O(2n) 지수시간 exponential time
def Bbit_print(i):
	output = ""
	for j in range(7, -1, -1):
		output += "1" if i & (1 << j) else "0"
	print(output)

for i in range(-5, 6):
	print("%3d = "%i, end='')
	Bbit_print(i)

...
-5 = 11111011
-4 = 11111100
-3 = 11111101
-2 = 11111110
-1 = 11111111
0 = 00000000
1 = 00000001
2 = 00000010
3 = 00000011
...

def Bbit_print(i):
	output = ''
	for j in range=(7, -1, -1):
		output += '1' if i & (1<<j) else '0'
	print(output, end='')

a= 0x10 # 16진수
x= 0x01020304
print('%d = ' % a, end = '')
Bbit_print(a)
print()
print('0%X = ' % x, end ='')
for i in range(0, 4):
	Bbit_print((x >> i*8) & 0xff)

엔디안(Endianness)

  • 컴퓨터의 메모리와 같은 1차원 공간에 여러 개의 연속된 대상을 배열하는 방법을 의미하며 HW 아키텍처마다 다름
  • 속도향상을 위해 바이트 단위와 워드 단위를 변환하여 연산할 때 올바로 이해하지 않으면 오류를 발생시킬 수 있음
  • 빅엔디안(Big-endian): 보통 큰 단위가 앞에 나옴. 네트워크
  • 리틀엔디안(Little-endian): 작은 단위가 앞에 나옴. 대다수의 데스크탑 컴퓨터

예)

0x1234를 빅엔디안으로는 12 34, 리틀엔디안으로는 34 12가 됨

 

  • 명제
    • 참이나 거짓을 알 수 있는 식이나 문장
    • p, q, r … 로 표현
    예) 서울은 대한민국의 수도다.
  • 1 + 1 = 3
  • 진릿값
    • 참이나 거짓을 표현
    • T, F 혹은 1, 0

연산(결합)

  • 부정 Not
    • p가 명제일 때, 명제의 진릿값이 반대
    • ~p 또는 -p로 표기 (not p 또는 p의 부정으로 읽음)
  • 논리곱 And
    • p, q가 명제일 때, p,q 모두 참일 때만 참이 되는 명제
    • p ^ q(p and q, p 그리고 q)
  • 논리합 OR
    • p, q가 명제일 때, p,q 모두 거짓일 때만 거짓이 되는 명제
    • p V q (p or q, p또는 q)
  • 배타적 논리합 XOR
    • p, q가 명제일 때, p, q 중 하나만 참일 때 참이되는 명제

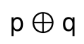
연산자 우선 순위

    • V, ^ > →, ←—→
  • 항진명제: 진릿값이 항상 참
  • 모순명제: 진릿값이 항상 거짓
  • 사건명제: 항진명제도 모순명제도 아닌 명제
  • 조건 명제
    • p, q가 명제일 때, 명제 p가 조건(또는 원인), q가 결론(또는 결과)로 제시되는 명제
    • p → q (p이면 q이다)
  • 쌍방조건명제
    • p, q가 명제일 때, 명제 p와 q가 모두 조건이면서 결론인 명제
    • p ↔ q (p면 q이고, q면 p다)
  • 조건명제의 역, 이, 대우
    • 역: q → p
    • 이: -p → -q
    • 대우: -q → -p
    예시)역: 치킨을 사주면 100점을 받는다대우: 치킨을 사주지않으면 100점이 아니다
  • 이: 100점을 받지 않으면 치킨을 사주지 않는다
  • 명제: 100점을 받으면 치킨을 사준다

수와 표현

  • 컴퓨터는 0/1을 표현할 수 있는 비트들을 모아 수를 표현
  • k개의 비트를 사용하면 0부터 2^k-1까지 표현 가능
  • 꼭 위와 같은 범위인 것은 아니고, 어떤 경우든 최대 2^k가지 값을 표현하는 것이 가능
  • 10진수로 k자리까지 쓰면 0부터 10^k-1까지 표현이 가능한 것과 완전히 동일한 과정
  • x = logn일 때 x와 n을 비교하면 x가 더 작고, n이 커질수록 그 차이가 굉장히 달라짐
  • 100자리로 표현할 수 있는 10진수 값은 읽을 수도 없을 정도로 큰 값
  • 컴퓨터분야에서 로그의 밑은 항상 2
저작자표시 (새창열림)