이전까지 다뤘던 부분들은 모두 단방향 로직이었다. 받아낸 아웃풋을 저장하지 않으면 컴퓨터가 제대로 동작할리 없는데, 이번엔 전자기기의 전원이 켜져 있을 때 단기간 저장을 해내는 메모리의 구조에 대해 다뤄볼까한다.
PC게임을 즐기며 성능에 관심이 있거나 관심을 가져야만 했던 상황을 경험해본 사람이라면 - 해보고 싶은 고사양 게임이 내 PC에서 구동될지 알아본다거나.. - 램이라는 하드웨어에 대해 들어봤을 것이다. Random Access Memory의 약자로, 기기의 전원이 켜져있는동안 데이터를 저장하는 부품이다. HDD, SSD 같은 지속성 메모리(persistent memory)가 전원 공급 없이도 보존되는 것과는 다르다. 지속성 메모리에 대해선 차후 다뤄보기로하고, 램에 대해 파헤쳐보자.

메모리의 기본은 저장된 출력값이 지속되는 것이다.
이전에 알아본 OR게이트, AND게이트를 통하여 우리는 항상 0 또는 1이 출력되는 회로를 만들 수 있다.
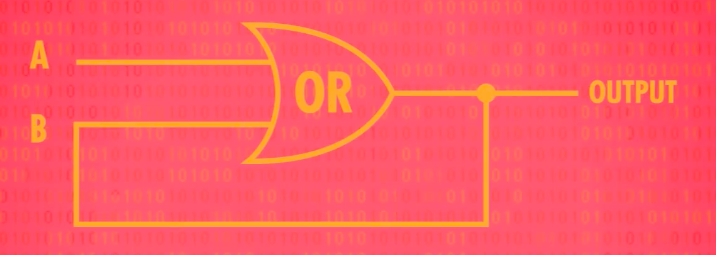
위와 같은 회로를 구성하면 A 인풋으로 1이 입력될 시 회로에 1이 저장되어 이후 인풋이 없어도 1을 항상 출력 받을 수 있다.
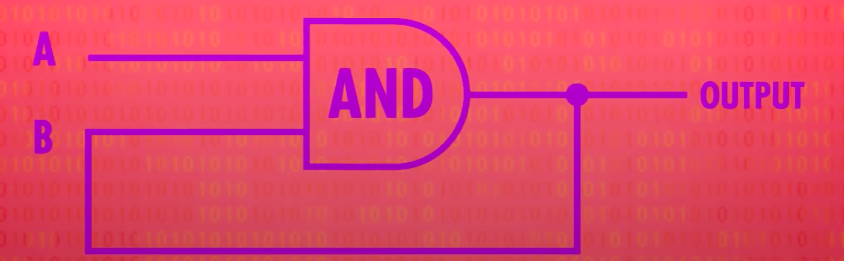
또한 위와 같은 회로를 구성하면 회로에 0이 저장되어 이후 인풋이 있든 없든 항상 0을 출력 받을 수 있다.
각각의 회로들은 출력값이 고정되어 메모리로의 활동도가 거의 없다시피한데, 제대로된 메모리 조각을 만들기 위해서는 둘을 결합하면 된다.

이미지 출처: soojong.tistory.com
이렇게 합쳐진 회로를 AND-OR Latch라고 부른다.
해당 랫치의 인풋은 set과 reset 두가지이다. 말하자면, 리셋의 입력값이 1일 때의 셋 입력값이 저장되며 이것이 아웃풋이 된다.
이제 우리는 1비트의 메모리를 저장하는 회로를 알게 되었다. 이를 좀 더 효율적으로 활용하기 위해서는 추가적인 로직 게이트들이 필요하다.

이미지 출처: Crash Course Computer Science
약간 복잡해졌지만 각 단계씩 뜯어서 생각해보면 이해가 빠르다.
결과적으로 Write Enable 인풋이 1일 때의 Data Input 값에 회로에 저장되어 일정한 아웃풋을 가지게된다.
쓰기 활성화 인풋을 가지게 되어 이는 Gate Latch라고 불린다.
이러한 게이트 랫치를 8개 이어 붙이면 1바이트를 저장할 수 있게 되는데, 이런 식으로 작동하는 랫치 그룹을 레지스터라고 불린다.
Write Enable에 대한 인풋 라인은 단 하나만 가지고도 병렬로 배치된 랫치들에 신호를 줄 수 있기 때문에 8비트의 레지스터에는 8개의 데이터 인풋라인, 8개의 아웃풋라인, 그리고 한개의 쓰기 활성화 라인을 가지게된다.
즉, 라인개수 = 랫치개수 * 2 + 1가 되는 것.
그렇기에 비트가 높아지면 과하게 많은 라인 수를 가지게 된다. 그런 번잡스러움을 피하기위해.. 또 머리 좋은 사람들이 해결책을 생각해냈다. 랫치를 열행 구조로 배치하고 가로 세로로 신호를 줘서 원하는 위치에 있는 랫치를 작동 시키는 것. 가로 신호와 세로 신호를 받는 and 게이트를 랫치의 데이터 인풋 라인에 꽂아주는 것이이다.
이 방법을 통하면 64비트의 레지스터에서 데이터를 읽고 쓰는데에 129개의 라인까지는 필요 없이 8개의 가로 라인, 8개의 세로 라인, 1개의 데이터 인풋 라인, 1개의 쓰기 활성화 라인, 1개의 읽기 활성화 라인으로 총 19의 라인만 있으면 충분해진다.
레지스터 내에서 필요한 랫치에 접근하기 위해서는 해당 랫치에 대한 이진수로된 주소값이 필요하다. 위의 사진에서도 나타냈듯 16개의 열행을 가지기에 이진수 네자리 + 네자리가 필요하다. 예를 들어, 12행 8열의 랫치에 접근하기 위해서는 12에 대한 이진수인 1100, 그리고 8에 대한 이진수인 1000을 붙여서 8비트인 11001000의 주소값이 필요한 것이다.

이렇게 만들어진 메모리 블럭이 다시 열행 구조로 쌓이면서 저장 가능 규모가 커진다.
열행 구조들을 통해 배치되어 좌표값으로 엑세스가 가능한 이러한 메모리를 Random Access Memory라고 부르며 우리가 사용하는 RAM 스틱 또한 그 깊은 내부는 이렇게 이루어져 있다.
'Computer Science' 카테고리의 다른 글
| [Computer Science] Arithmetic Logic Unit(ALU)는 어떻게 작동할까 (0) | 2022.11.29 |
|---|---|
| [Computer Science] 숫자와 문자의 이진수 표현 (2) | 2022.11.24 |
| [Computer Science] 머신러닝, 딥러닝은 쉽게 말해.. (0) | 2022.11.13 |
| [Computer Science] 이진수 연산의 로직 게이트 (0) | 2022.11.09 |
| [Computer Science] 전자컴퓨팅의 여명 (0) | 2022.11.01 |